【计算机视觉】用于计算机视觉的深度学习和卷积神经网络

在CNN的卷积和池化层内部

为什么我们在人工智能中使用生物学概念和术语“神经网络”来解决实时问题？

在20世纪中期对猫进行的一项实验中，研究人员Hubel和Wiesel确定，神经元在结构上是这样排列的，即一些神经元在暴露于垂直边缘时会发光，另一些则在暴露于水平或对角边缘时发光。用于特定任务的专用组件的概念是卷积神经网络（CNNs）解决人脸识别或图像对象检测等问题的基础。

卷积和滤波器

卷积是两个函数的运算，产生第三个函数和结果输出函数。它是通过从不同级别的图像中提取特征来实现的。特征可以是边、曲线、直线或任何类似的几何特征。

细胞神经网络使用滤波器——本质上是数字阵列——进行特征识别。滤波器应具有与其输入相同的深度；因此，表示图像的6×6阵列应该具有6×6滤波器。滤波器也称为神经元或核。

考虑在CNN中使用滤波器进行特征识别的示例。下面的示例过滤器检测图像中的一条直线：

用于检测直线的过滤器

在下面的图像中，相同的过滤器应用于两个不同的图像。

第一个图像包含一条手绘线——数字1——和一个表示它的数组：

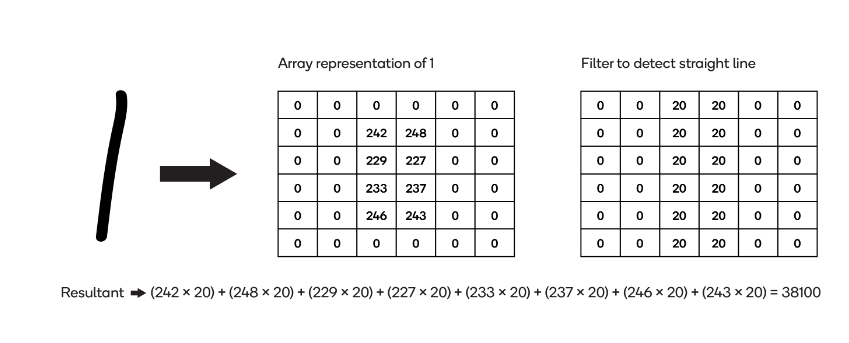
对具有直线的图像应用过滤器

两个数组的乘积之和（“结果”）为38100。

下一个图像包含手绘数字2（不是直线）和表示它的数组：

对没有直线的图像应用过滤器

数组中与过滤器中对齐的非零条目较少，因此结果28700远低于第一个图像中的结果。

这说明了CNN的过滤。下图描述了一个样本卷积神经网络的架构。

CNN架构

以下是描述细胞神经网络时常用的术语。

激活

激活是用于获得神经网络中节点输出的函数。在细胞神经网络中，激活函数表示结果的线性或非线性。它们将结果映射到（0，-1）或（-1，1）。常用的激活函数有sigmoid、tanh和Relu。

功能图

卷积过程的结果被称为特征图。下面显示的是一个计算卷积运算输出维度的公式：

• An image matrix (volume) of dimension (h × w × d)
• A filter (f_h × f_w × d)
• Outputs a volume dimension (h – f_h + 1) × (w – f_w + 1) × 1

大步走 （Stride）

Stride描述了内核在图像上水平和垂直移动以执行完整卷积运算的位置数。

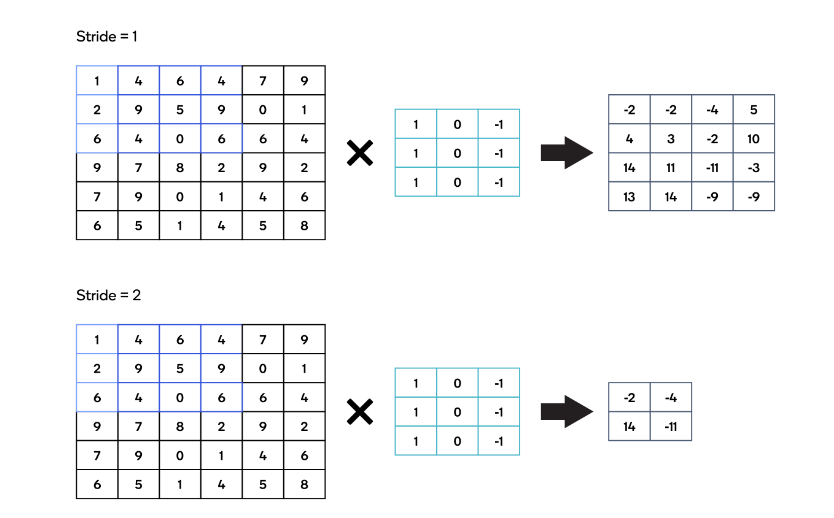
大步走

Pooling

池用于减小表示的空间大小。它是在特征图上执行的。

最大池化和平均池化是最常用的池化方法。池化操作在卷积操作之后执行，以在表示进入下一层之前减小表示的输入大小。

Pooling in CNN

压扁层：Flattened layer

平坦层用于将n维向量转换为一维向量。在我们的例子中，我们将结构化的二维图像转换为一维向量，这是神经网络的输入层。

完全连接层:Fully connected layer

完全连接层将一层的每个神经元连接到另一层的每一个神经元。为激活函数给出了全连通层的最后一层，从而有助于分类。