【数据分析】基于仿真的优化

基于仿真的优化（也称为简单的仿真优化）将优化技术集成到仿真建模和分析中。由于仿真的复杂性，目标函数的评估可能变得困难且昂贵。通常，基础仿真模型是随机的，因此必须使用统计估计技术（在仿真方法中称为输出分析）来估计目标函数。

一旦系统被数学建模，基于计算机的模拟就会提供有关其行为的信息。参数仿真方法可用于提高系统的性能。在这种方法中，每个变量的输入都是变化的，其他参数保持不变，并观察对设计目标的影响。这是一种耗时的方法，可以部分提高性能。为了以最小的计算量和时间获得最优解，迭代求解问题，在每次迭代中，解都更接近最优解。当涉及多个目标时，这些方法被称为“数值优化”、“基于模拟的优化”[1]或“基于仿真的多目标优化”。

在仿真实验中，目标是评估不同输入变量值对系统的影响。然而，有时人们的兴趣在于根据系统结果找到输入变量的最佳值。一种方法是对所有可能的输入变量进行模拟实验。然而，由于多种可能的情况，这种方法并不总是实用的，而且它只会使为每种情况运行实验变得困难。例如，输入变量可能有太多的可能值，或者模拟模型可能过于复杂和昂贵，无法运行大量的输入变量值。在这些情况下，目标是迭代找到输入变量的最优值，而不是尝试所有可能的值。这个过程称为模拟优化。2.

根据决策变量类型，可以根据图1选择具体的基于模拟的优化方法。3.

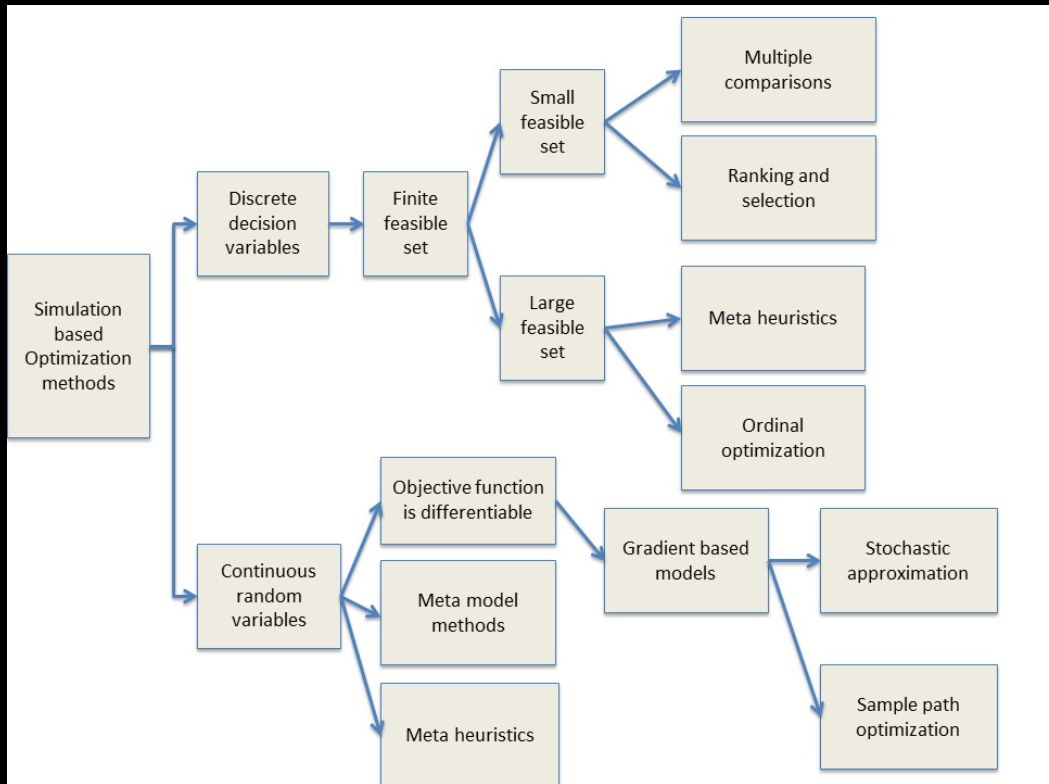
图1根据变量类型对基于仿真的优化进行分类
优化存在于运筹学的两个主要分支中：

• 优化参数（静态）-目标是找到参数的值，这些值对于所有状态都是“静态的”，目的是最大化或最小化一个函数。在这种情况下，可以使用数学规划，如线性规划。在这种情况下，当参数包含噪声或问题评估因其复杂性而需要过多的计算机时间时，模拟会有所帮助。4.
• 优化控制（动态）-这主要用于计算机科学和电气工程。最优控制是针对每个状态的，每个状态的结果都会发生变化。人们可以使用数学规划，也可以使用动态规划。在这种情况下，模拟可以生成随机样本并解决复杂和大规模的问题。4.

基于仿真的优化方法

下面讨论了仿真优化中的一些重要方法。[5] [6]

统计排名和选择方法（R/S）

排序和选择方法是针对备选方案固定且已知的问题而设计的，并使用模拟来估计系统性能。在仿真优化设置中，适用的方法包括无差异区方法、最优计算预算分配和知识梯度算法。

响应面法（RSM）

在响应面方法中，目标是找到输入变量和响应变量之间的关系。该过程从尝试拟合线性回归模型开始。如果P值很低，则将实现通常为二次的高次多项式回归。每个模拟测试都将进行寻找输入和响应变量之间良好关系的过程。在仿真优化中，响应面法可用于找到在响应变量方面产生预期结果的最佳输入变量。7.

启发式方法

启发式方法通过速度改变准确性。他们的目标是在解决问题太慢或失败时，比传统方法更快地找到一个好的解决方案。通常他们会找到局部最优值，而不是最优值；然而，这些值被认为与最终解足够接近。这类方法的例子包括禁忌搜索和遗传算法。4.

元模型使研究人员能够获得可靠的近似模型输出，而无需运行昂贵且耗时的计算机模拟。因此，模型优化过程可以减少计算时间和成本。8.

随机近似

当函数不能直接计算，只能通过噪声观测进行估计时，使用随机近似。在这些场景中，此方法（或方法族）会查找这些函数的极值。目标函数为：[9]

无导数优化方法

无导数优化是数学优化的一门学科。该方法应用于某个优化问题，当其导数不可用或不可靠时。无导数方法基于样本函数值建立模型，或者直接绘制函数值的样本集，而无需利用详细的模型。由于它不需要导数，因此不能与基于导数的方法进行比较。[10]

对于无约束优化问题，其形式如下：

无导数优化的局限性：

1.一些方法不能处理具有多个变量的优化问题；结果通常不那么准确。然而，在许多实际案例中，无导数方法在非平凡的模拟优化问题中取得了成功，这些问题包括目标函数中表现为“噪声”的随机性。例如，请参见以下[5]。[11]

2.当面对最小化非凸函数时，它将显示出其局限性。

3.无导数优化方法相对简单易行，但与大多数优化方法一样，在实际实现中需要注意（例如，在选择算法参数时）。

动态规划与神经动态规划

动态规划
动态规划处理分阶段做出决策的情况。解决这类问题的关键是权衡当前和未来的成本。[12]

一个动态基本模型有两个特征：

1） 它具有离散时间动态系统。

2） 成本函数随着时间的推移是累加的。

对于离散特征，动态规划的形式如下：

神经动态规划

神经动态规划与动态规划相同，除了前者具有近似架构的概念。它结合了人工智能、仿真基础算法和功能方法技术。这个术语中的“Neuro”起源于人工智能界。这意味着学习如何通过基于当前行为的内置机制为未来做出更好的决策。神经动态规划最重要的部分是为最优问题构建一个训练好的神经网络。[13]

局限性

基于仿真的优化有一些局限性，例如难以创建一个模型，以一种被认为足够好的方式模拟系统的动态行为。另一个问题是确定现实世界系统和仿真的不可控参数的复杂性。此外，只能获得实际值的统计估计。确定目标函数并不容易，因为它是测量的结果，这可能对解决方案有害。[14][15]