【图形计算】如何使用图论解决神秘圣诞老人问题

让我们谈谈图、哈密顿循环、NP 问题和回溯搜索。

每年我们家都会举办一次秘密圣诞老人活动。我们没有给每个家庭成员送一件廉价的廉价礼物，而是随机分配接收者，这样每个人都可以从一位匿名的圣诞老人那里得到一份好而有价值的礼物。

我们决定开发一个简单的网站，每个家庭成员都可以在其中注册、填写他们的愿望清单并在活动开始时获得接收者的姓名。为此有很多网站和应用程序，但我们决定拥有自己的服务来对排序算法进行一些修改。

在每个参与者都注册后，我们需要运行一个排序算法来决定谁送礼物给谁。为了解决神秘圣诞老人问题，我们需要找到这个排序算法。

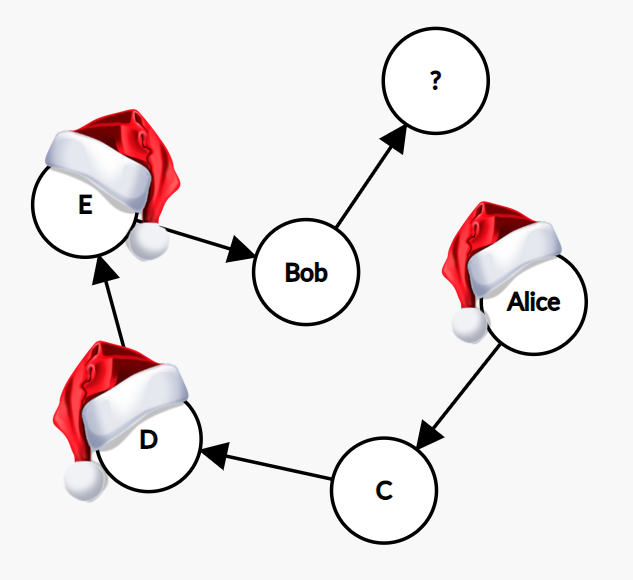
我们有一系列的所有参与者。让我们随机选择第一个。假设我们有鲍勃。接下来，我们从初始数组中删除 Bob，并从中随机抽取一个参与者。假设我们得到爱丽丝。所以，鲍勃给了爱丽丝一份礼物。然后从数组中移除 Alice 并随机获得一个参与者，该参与者将成为 Alice 的接收者。等等。重复直到初始数组为空。最后一位参与者将是鲍勃的秘密圣诞老人，他是第一位的。圣诞老人的链条是完整的。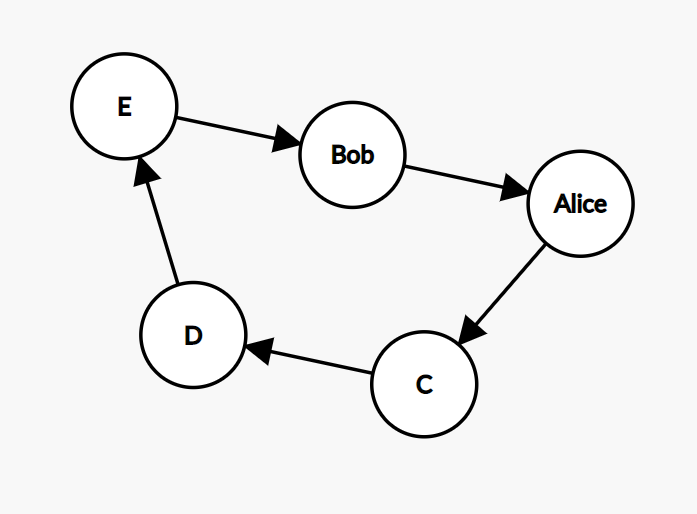

这样的算法被称为朴素。每一步都很明显，它模仿人们从帽子或彩票机中取出代币。在大多数情况下，朴素算法不是最优的并且没有很好的性能，但是这个任务非常容易，以至于朴素算法是最优的，并且具有 O(n) 的性能和 O(1) 的内存。

下一步是修改问题并向我们的算法添加一些额外的要求。这就是我们想要创建自己的服务的原因。有时，通过纯随机，您可以获得一个由于某种原因不能成为秘密的秘密圣诞老人。例如，如果我的圣诞老人是我的妻子，几乎不可能保守秘密。

因此，我们决定为问题添加约束。例如，Alice 和 Bob 登录了活动，但不想互相赠送礼物。我们需要将此数据添加到算法中并考虑这些约束。我们可以稍微修改算法：当我们需要为有约束的参与者（例如 Bob）选择接收者时，我们从参与者池中删除这些约束（Alice）并像以前一样随机选择一个。

有了这样的限制，我们的幼稚算法在某些情况下可能会失败。如果这是算法的最后一步，我们需要为 Bob 选择一个接收者，而 Alice 是池中唯一剩下的选项怎么办？在这种情况下，如果我们应用所有约束，将没有可供选择的选项，因此将没有解决方案。

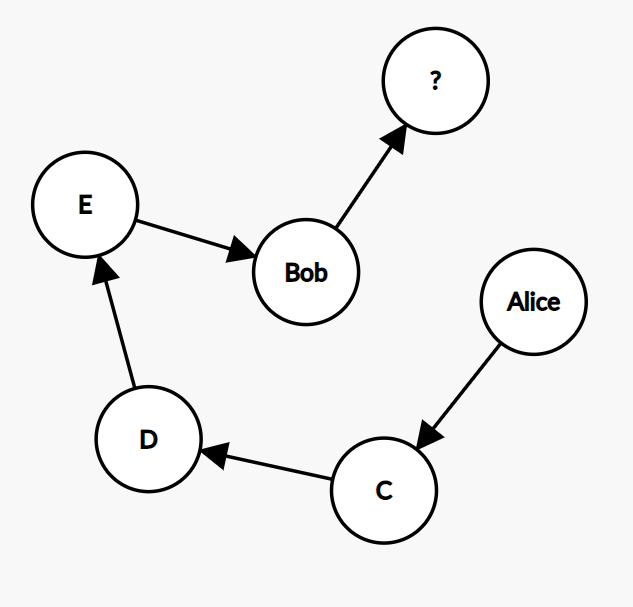
我们该如何解决？ 这里最简单的方法是重新启动算法，直到我们得到解决方案。 如果约束很少，它应该是非常安全的。 实际上，我们在 web 服务的第一个版本中就以这种方式修复了它。 它对 10 名参与者和几个限制条件非常有效，并且一次运行就找到了解决方案。 有时它需要 1 或 2 次重启，但没有无限循环。

但对于我们最初的问题，这是一个肮脏的解决方案。 让我们找到一个合适的算法来解决任何输入数据的这个问题。 可能，我们需要使用它的另一种表示。

我们有参与者。 我们还知道不想互相赠送礼物的参与者的限制（如果有的话）。 当我们有一些对象和它们之间的联系时，就该考虑图形了。

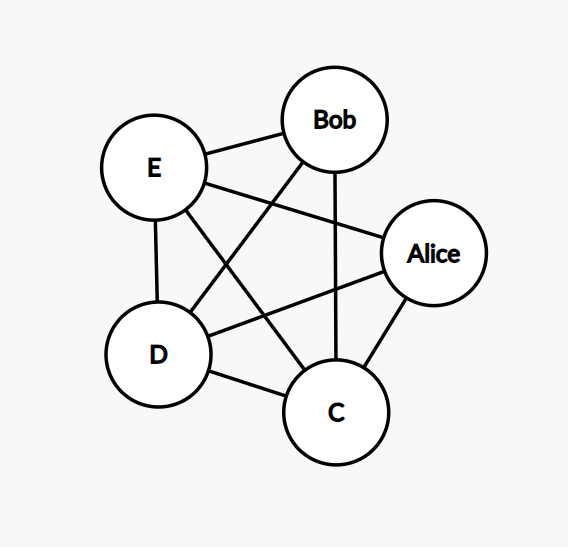
在这张图中，节点是参与者，节点之间的联系表明它们可以互相赠送礼物。 Bob 和 Alice 无法做到这一点，因此他们之间没有直接联系。

现在我们可以看到我们的解决方案是该图上的一条路径。它必须从任何一个节点开始，然后每个节点恰好经过一次，然后又回到起点，所以这意味着路径实际上是一个循环。恰好一次通过所有节点的路径称为哈密顿路径。因此，这样的循环是哈密顿循环。

这意味着秘密圣诞老人问题基本上是一个哈密顿循环问题，我们可以在书本或互联网上找到正确的算法。

好的，谷歌，如何在图中找到哈密顿循环？

但是谷歌让我失望了。显然，没有快速算法可以在图中找到哈密顿路径或循环。这是一个 NP 问题（非确定性多项式），这意味着它没有多项式算法。

更著名（或臭名昭著）的 NP 问题是旅行商问题（简称 TSP）：

给定一个城市列表和每对城市之间的距离，访问每个城市一次并返回起点城市的最短路径是什么？

听起来很熟悉，不是吗？我们需要准确地访问每个节点一次并返回初始节点。这基本上是我们这里的哈密顿循环。 TSP 没有快速的解决方案。人们撰写有关如何更快解决问题的科学论文。有些人使用启发式方法来减少蛮力搜索中的选项数量。有些人使用动态规划将其拆分为更容易解决的子问题。

这是否意味着我们的秘密圣诞老人问题需要如此复杂的算法？不，这要容易得多。这里的主要区别在于，旅行商问题需要一个最优的哈密顿循环（最短或最有利可图），而秘密圣诞老人问题需要任何哈密顿循环。

为了暴力破解 TSP，我们需要找到所有可能的周期并选择最优的。可能的循环数是用阶乘函数计算的：从 1 到 N 的所有整数相乘。如果我们在图中有 5 个节点，那么将有 120 个循环进行暴力破解。对于 10 个节点，将有 3628800 个选项。对于 20 个节点：2432902008176640000。很多。

我们的问题要简单得多。图中有很多合适的循环，我们需要找到第一个合适的。蛮力现在没那么可怕了。

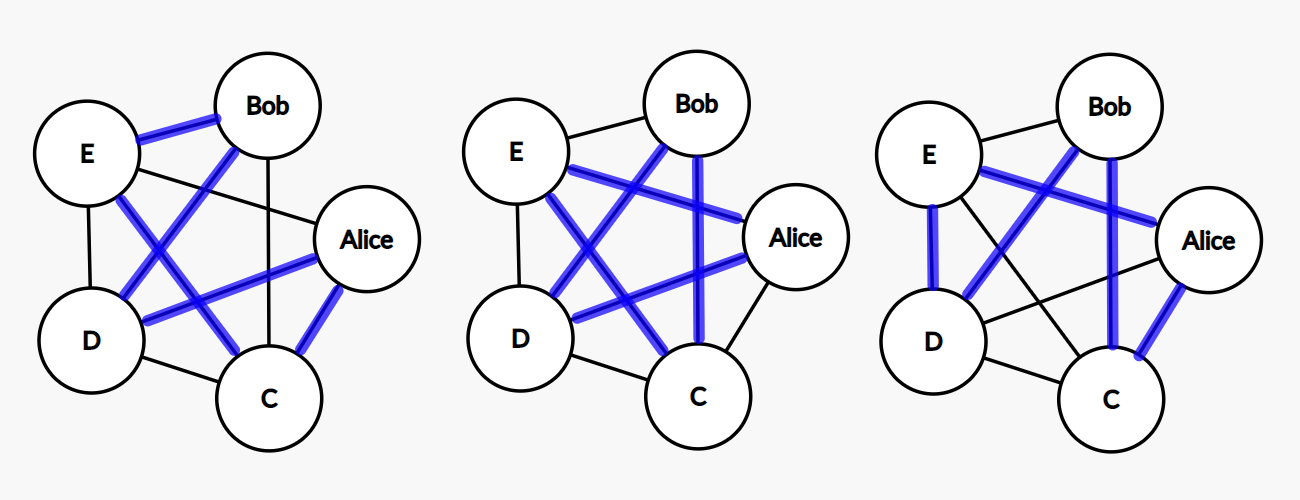
Examples of Hamiltonian cycles in the graph for Alice, Bob, and their friends

让我们弄清楚算法。 我们的目标是使用蛮力在图中找到一个哈密顿循环。 我们从一个随机节点开始。 这个节点有一些连接的节点。 我们随机选择它的一个邻居然后去那里。 这个节点也有连接的节点。 我们选择其中一个还没有被访问过。 等等。

在某些步骤中，我们可以发现没有可供选择的节点。 如果没有更多的连接（由于限制）或所有相邻节点都已被访问，则可能会发生这种情况。 这个问题看起来像我们在朴素算法中遇到的问题。 有了图表，我们可以更清楚地退后一步，选择另一个随机节点。 如果我们后退了一步，但仍然没有节点可供选择，我们再后退一步。

重复，直到我们访问所有节点并返回第一个节点。 循环完成。

这种搜索称为回溯搜索或深度优先搜索。

让我们看一个例子。

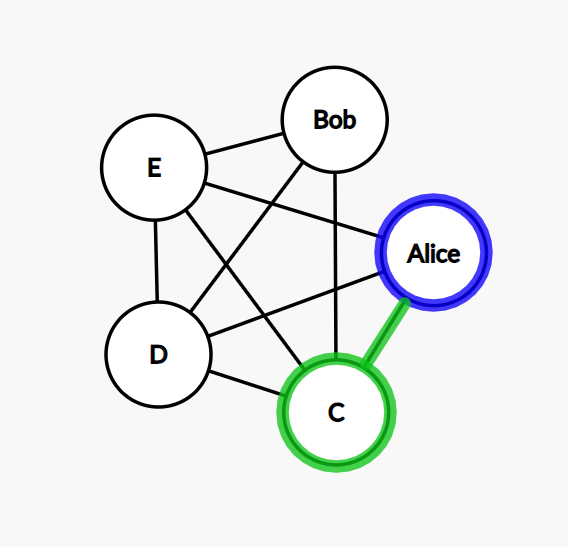
Step 3: then we pick the node D.

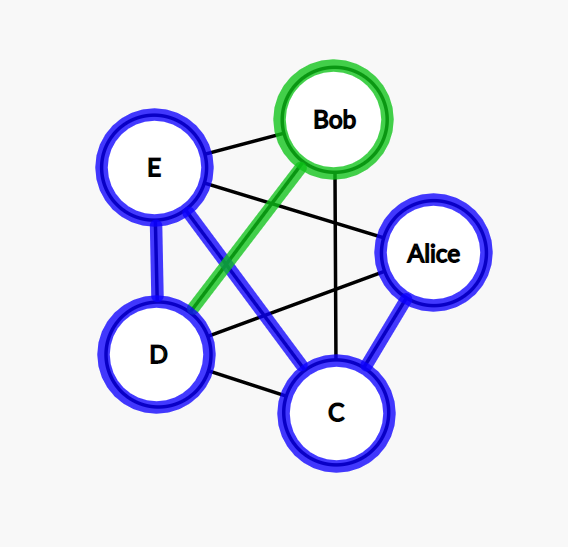
Step 4: the only node left to go from D is Bob. All the other nodes have been visited already.

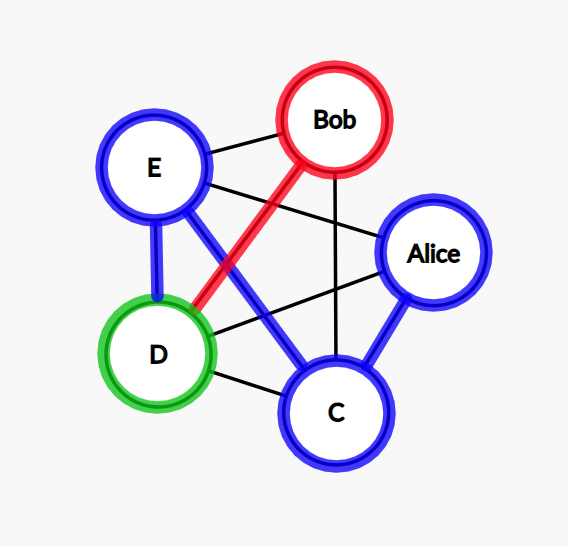
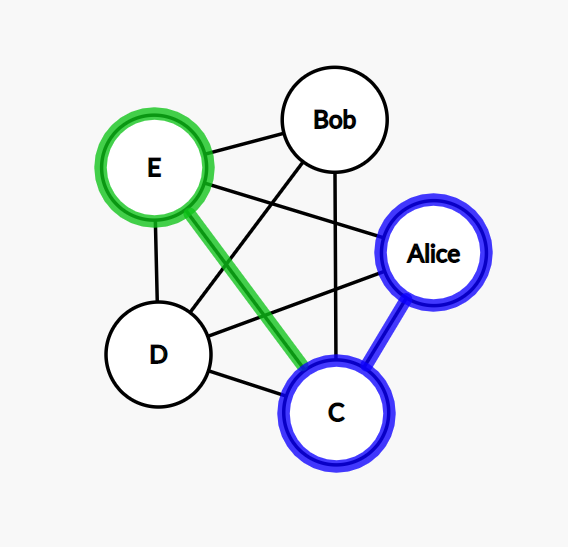
Step 5: our path contains all the nodes, and we need to go to the node Alice and finish the cycle, but there is no connection between Bob and Alice. We need to do a step back, so we return to D.

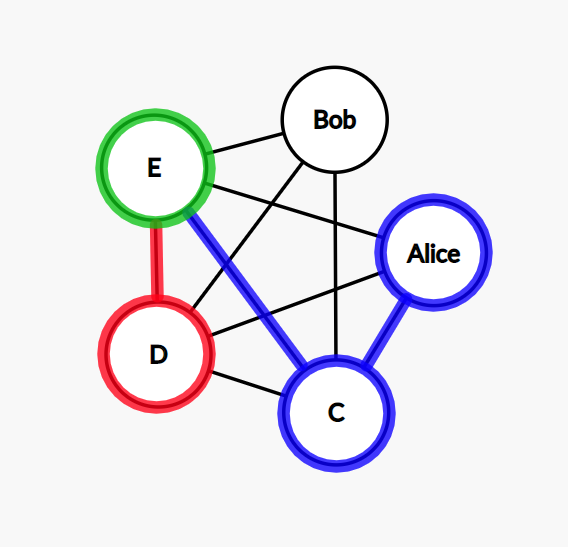
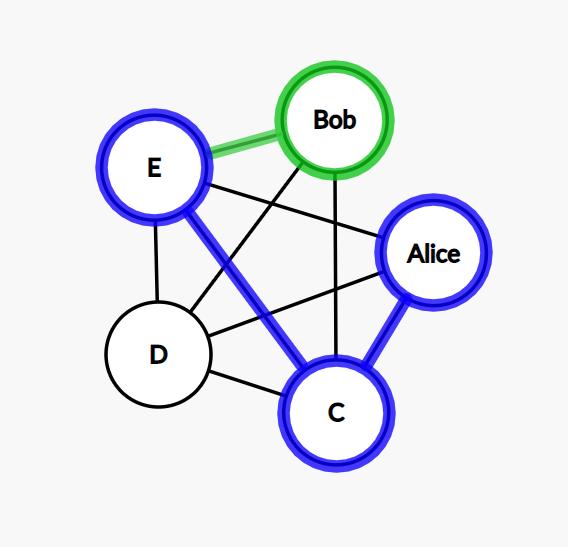
Step 7: this time, we go from E to Bob.

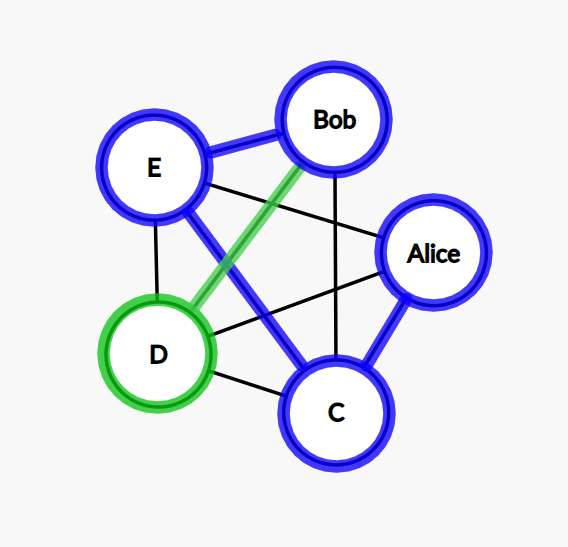
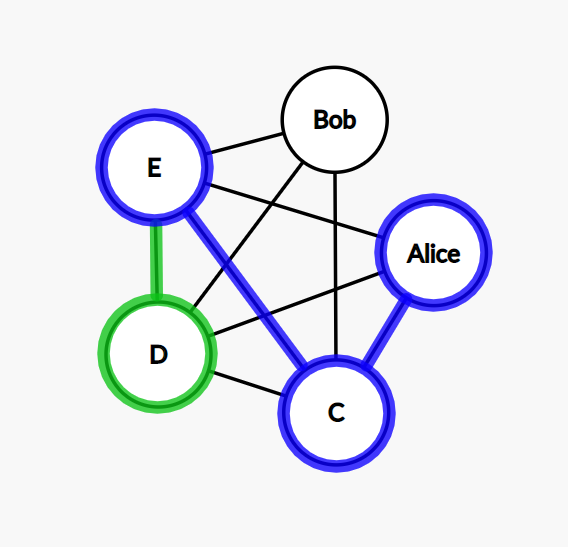
Step 8: the only possible move is from Bob to D now.

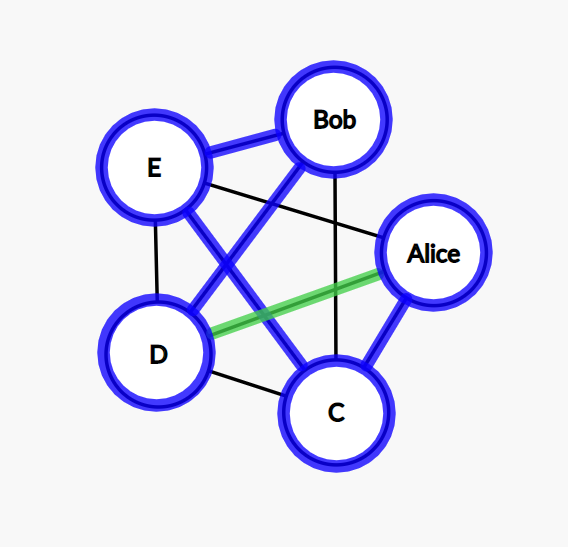
Step 9: we can go from D to Alice now. The cycle is complete. We found a solution.

如果我们总是找到一个死胡同，并且在多次回溯之后，我们返回第一个节点而没有成功找到哈密顿圈，那么这个图就没有解决方案。这是最坏的情况，因为我们需要暴力破解所有路径以验证没有合适的循环。而且很多，记住阶乘函数。

但我们正在解决特定网络服务的神秘圣诞老人问题。这实际上是一项工程任务，而不是数学任务。只有当约束太多，并且图中没有足够的连接来找到合适的循环时，才可能使算法失败。

如果我们有一个秘密圣诞老人活动会很可疑，并且一些参与者决定他们不想看到几乎所有其他人都是他们的圣诞老人。我们可以为界面添加一些限制，并定义每个参与者最多可以有 3 个约束。这对每个人来说都足够了，它将防止算法暴力破解数百万条路径。

我做了一些测试。使用 3 个约束的算法有时需要进行 1 或 2 次回溯，但对于大多数情况，它会在 N 步中为 N 个参与者找到解决方案。如果有更多的约束，情况会变得更糟。例如，有 100 个参与者和每个参与者 50 个约束，蛮力有时需要 100 步，有时需要 400000 步，有时需要 1500000 步。

我们最初的问题已经解决，我们有了一个具有稳定排序算法的工作网络服务。即使有数千名参与者，它的运行速度也足够快，这对于家庭范围的活动来说已经绰绰有余了。我们学到了一些关于哈密顿循环、NP 问题和深度优先回溯搜索的知识。

原文：https://medium.com/pragmatic-computer-science/how-to-solve-the-secret-s…

本文：https://jiagoushi.pro/node/2071