【安全技术】理解零知识证明：第 5 部分

语言 Chinese, Simplified

SEO Title

Understanding Zero-Knowledge Proofs: Part 5-Arithmetic Circuits and R1CS

category

安全技术

在之前的文章中，我们研究了一些隐私敏感的可验证计算的零知识证明的基础知识。在第 4 部分中，我们研究了如何为多项式知识生成证明。在这篇文章中，我们将讨论如何从一般计算转向代数方程（例如可以为其生成零知识证明的多项式方程）。

算术电路：算术电路是一种将计算表示为有向无环图的方式，其中输入节点是变量和常量，中间节点是加法或乘法。算术电路的输出将是输入变量的某个多项式函数。请注意，这些算术电路在给定的有限域 Fp 上进行操作，加法和乘法运算以 p 为模。事实证明，这种表示足够强大，可以捕获非常一般的计算。让我们考虑几个例子。

假设您想捕获关系 w=v/u。虽然运算仅限于加法和乘法，但可以通过添加新变量用以下电路来表示。

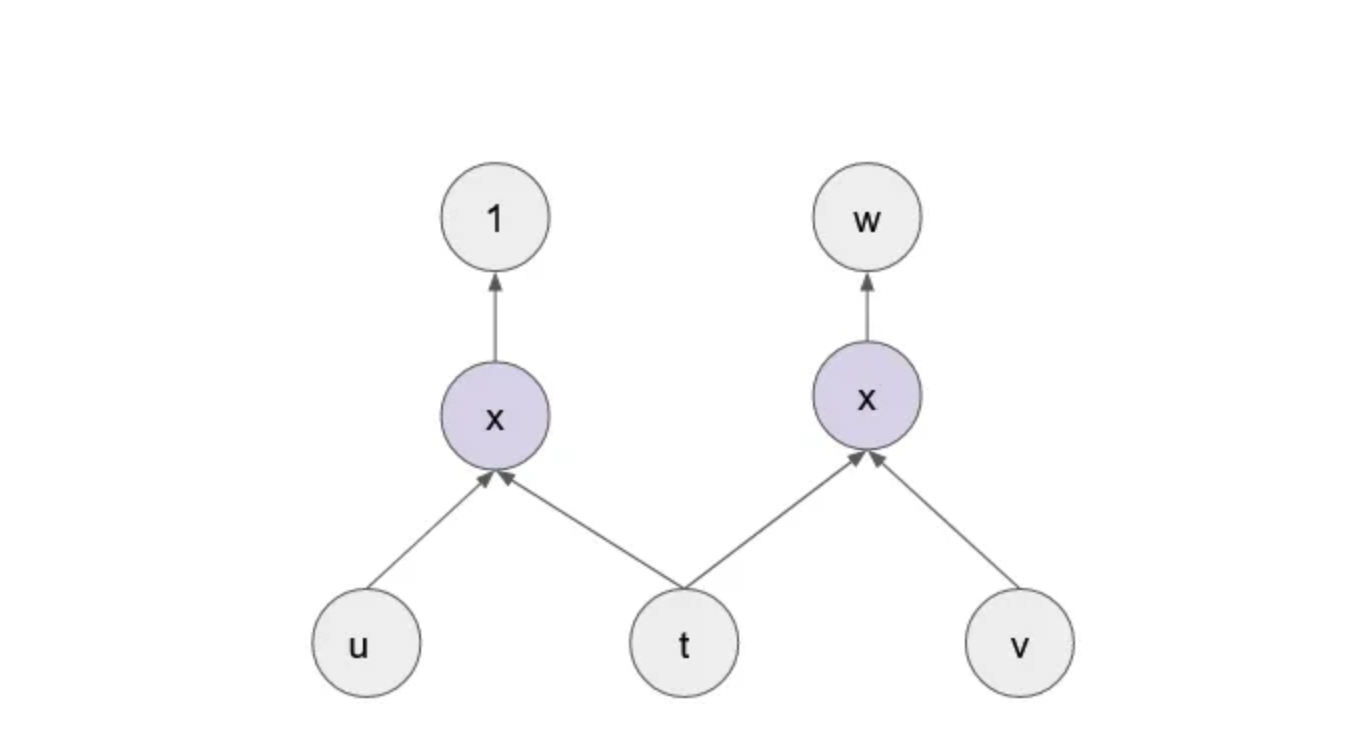
表示除法的算术电路：w = v/u。请注意，u*t = 1 => t = u^-1。因此 w = v*t = v*u^-1 = v/u
经过一些努力，其他运算（包括布尔运算、条件以及其他计算原语）也可以表示为算术电路。以下电路确保 b 是布尔变量。

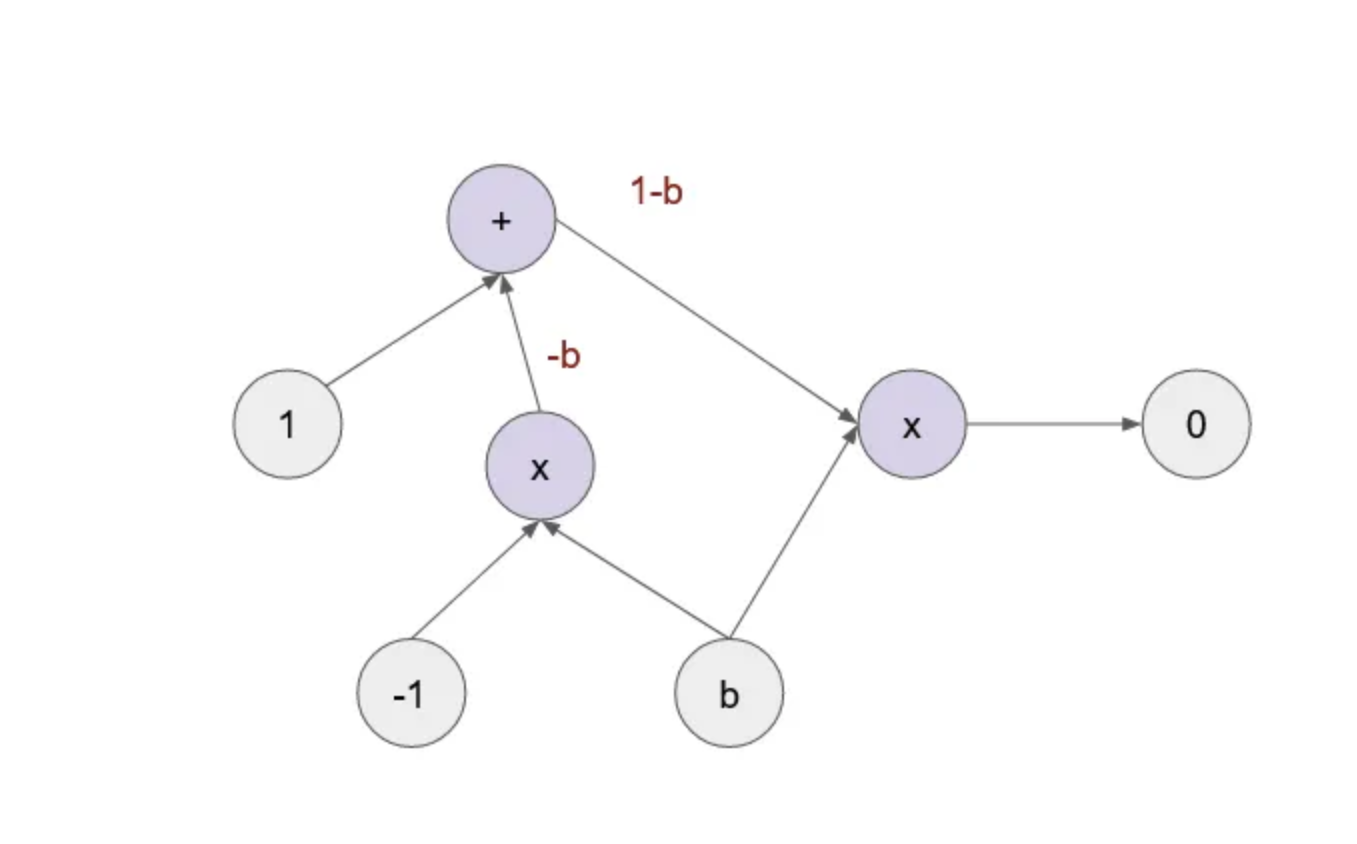
该算术电路通过确保 b*(1-b) = 0 来确保 b 是布尔变量。
以下显示了另一个实现条件语句的算术电路示例：如果 b 则 w = u + v，否则 w = u * v，其中 b 是布尔变量。我们看到它把上面的电路当成了一个“小工具”（这个电路虚线左边的部分和上面的一样）。

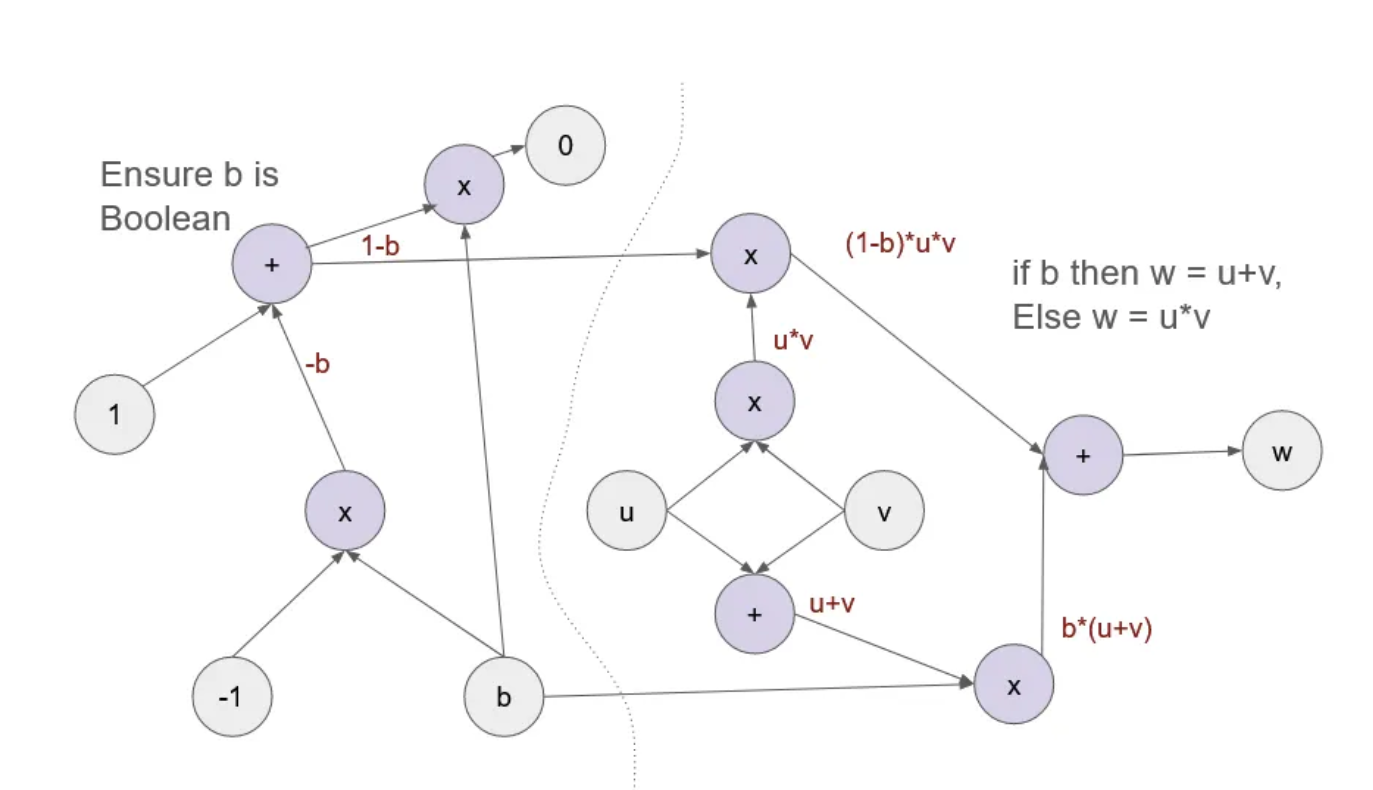
算术电路实现条件计算，其中条件被约束为布尔值。
等级 1 约束系统 (R1CS)：算术电路表示的标准中间格式称为等级 1 约束系统。R1CS 是一系列方程，形式如下：

s·A * s·B = w·C。

这里，A、B、C、s 都是向量，“·”运算是相应两个向量的标量点积，* 是乘法。

让我们举一个简单的例子：考虑方程 w = 3u² + 2v。我们可以将其表示为 3u² = (w — 2v) => [0 0 3 0]·[1 w u v]*[0 0 1 0]·[1 w u v] = [0 1 0 -2]·[1 w u v]，这是所需的形式，其中 s = [1 w u v]，A= [0 0 3 0]，B= [0 0 1 0]，C= [0 1 0 -2]。请注意，s 本质上是电路中变量的集合，常数项为单个 1。

对于更复杂的计算，将有多个这样的 R1CS 方程。考虑我们之前给出的代数电路示例，将条件语句编码为 b*(u+v) + (1-b)*(uv)，其中 b 是一个布尔值，表示为 b*(1-b)=0。这可以转换为以下方程：
b*(1-b) = 0 ; b*(u+v) = t1 ; uv = t2 ; (1-b)*t2 = t3 ; (t1+t3) = w
如果我们考虑 s = [1 b u v t1 t2 t3 w]，我们可以用 R1CS 形式表达上述每一个，只给出上述五个方程的三个向量 A、B、C，如下所示（尝试自己验证它们是如何产生的）：
[0 1 0 0 0 0 0 0], [1 -1 0 0 0 0 0 0], [0 0 0 0 0 0 0]
[0 1 0 0 0 0 0], [0 0 1 1 0 0 0 0], [0 0 0 0 1 0 0 0]
[0 0 1 0 0 0 0 0], [0 0 0 1 0 0 0 0], [0 0 0 0 1 0 0 0], [0 0 0 0 0 1 0 0]
[1 -1 0 0 0 0 0 0], [0 0 0 0 0 1 0 0], [0 0 0 0 0 0 1 0]
[0 0 0 0 1 0 1 0], [1 0 0 0 0 0 0 0], [0 0 0 0 0 0 1]

一般来说，系统中的 R1CS 约束数量将等于给定算术电路中的非常量乘积数量。

向量 s 称为见证。假设我们使用输入 b = 1、u = 0、v = 2 运行上述计算。我们看到条件 b 为布尔值且为真将导致 w = u+v = 2。并且可以确定中间值 t1、t2、t3 以及 t1 = 2、t2 = 0、t3 = 0。见证的对应值将是 [1 1 0 2 2 0 0 2]。我们可以粗略地将此见证视为证据，证明整个计算是在给定的输入下运行的，并生成了正确的中间值和输出。如果给定的见证满足所有 R1CS 约束，则它对应于给定算术电路的正确执行。（例如，如果提供了错误的见证，其对应于 b 的第二个元素中包含 2，则它将无法通过验证，因为对应于 b*(1-b)=0 的第一个约束将不成立，即因为 b 不是它本应是的布尔 0/1 值。同样，如果提供了错误的见证，其中 b = 1，u 和 v 设置为 0 和 2，t1 = 2，t2 = 0，t3 = 0，但 w = 3，则它将无法通过对应于 (t1+t3) = w 的验证。）

附加说明：R1CS 最初由 Ben Sasson 等人于 2013 年定义如下：

Ben Sasson 等人在 2013 年对 R1CS 的早期定义（称为秩 1 二次方程）

在 2019 年关于 Aurora 的论文中，作者解释了 R1CS 的好处：“我们选择 R1CS 是因为它达到了一种有吸引力的平衡：它通过允许“本机”字段算术和没有扇入/扇出限制来概括电路，但它足够简单，可以为其设计有效的参数系统。此外，R1CS 已展示出强大的经验价值：它是现实世界系统的基础，并且有编译器可以减少程序执行……这导致了学术界和工业界努力标准化 R1CS 格式。”

下一篇文章：接下来，我们将讨论如何将 R1CS 转换为二次算术程序，从而简化以多项式求值形式进行的算术电路验证。