【零知识证明】理解零知识证明：第四部分——多项式承诺

在本系列的第 2 部分中，我们介绍了密码学所需的一些基本数学背景，即有限域、循环群和椭圆曲线，在第 3 部分中，我们讨论了椭圆曲线密码学 (ECC) 和双线性配对的概念。在本部分中，我们将通过了解多项式承诺，最终开始深入了解零知识证明，特别是零知识简洁非交互式知识论证 (zk-SNARK) 的工作原理。

为了撰写本文，我借鉴了许多资料，包括 Maksym Petkus 的文章“zk-SNARK 的工作原理和原理”、Ben Bencik 的多项式承诺以及这篇关于 KZG 承诺方案的文章。关于该主题的另一个有用参考资料是 Dankrad Feist 关于 KZG 多项式承诺的文章。

验证多项式知识

为什么是多项式：首先，考虑实数的多项式函数。多项式的一个特性是两个 d 次多项式最多可以在 d 个点相交。（这是因为如果将它们相等，则会得到最多 d 次的多项式方程，该方程最多可以产生 d 个不同的实根。）这意味着，如果您在任意点处求多项式的值，则另一个多项式在该点具有相同值的可能性极小。因此，可以通过在任意点处测试某个多项式来评估某人声称他们以高概率知道该多项式的说法。

上述结果也通过 Schwartz-Zippel 引理推广到有限域。引理陈述如下：设 P() 是域 F 上 n 个 d 度变量的非零多项式。设 S 是 F 的有限子集。如果从 F 的有限子集 S 中均匀且独立地随机选择多项式的 n 个参数 (r_1、r_2、… r_n)，则 P(r_1、r_2、… r_n) = 0 的概率最多为 d/|S|。这可用于表明两个不同的多项式在随机选择的点上一致的概率可以任意低（通过选择足够大的集合 S）。这将多项式知识的证明简化为某一点的多项式知识的证明，从而实现简洁性 — — 这是 zk-SNARK 的关键属性之一。

多项式知识的证明：假设我们有一个 d 度多项式 f(x)，其属性为 f(a) = b。我们希望证明者生成一个证明，证明它知道 f(x) 并且已经计算出 f(a) = b。这相当于要求证明者证明存在某个商多项式 w(x)，可以将其表示为比率：w(x) = (f(x)-b)/(x-a)。

（为什么？因为它意味着 f(x)-b = w(x)(x-a)。这恰恰表明当 x=a 时，f(x)-b = 0 => f(a)=b。）

根据我们上面所说的，对于给定点 s，证明者很可能只需证明 w(s) = (f(s)-b)/(s-a) 就足够了。

现在有一个微妙之处需要考虑。在提供和确定 w(s) 时，不应允许证明者知道 s 是什么，并且应提前对 f(s) 做出承诺。否则，他们可以简单地编造一些任意的 f’(s) != f(s) 并返回满足（错误）方程 w’(s) = (f’(s) — b)/(s-a) 的任意 w’(s)。

相反，我们希望让证明者访问加密版本的 s 和加密版本的 f(s)，并让其基于此生成证明，然后验证者可以检查该证明。这就是下面描述的方案中所做的，该方案被称为 KZG 多项式承诺方案，因为它首次出现在 Aniket Kate、Gregory Zaverucha 和 Ian Goldberg 于 2010 年发表的一篇论文中。

KZG 多项式承诺方案

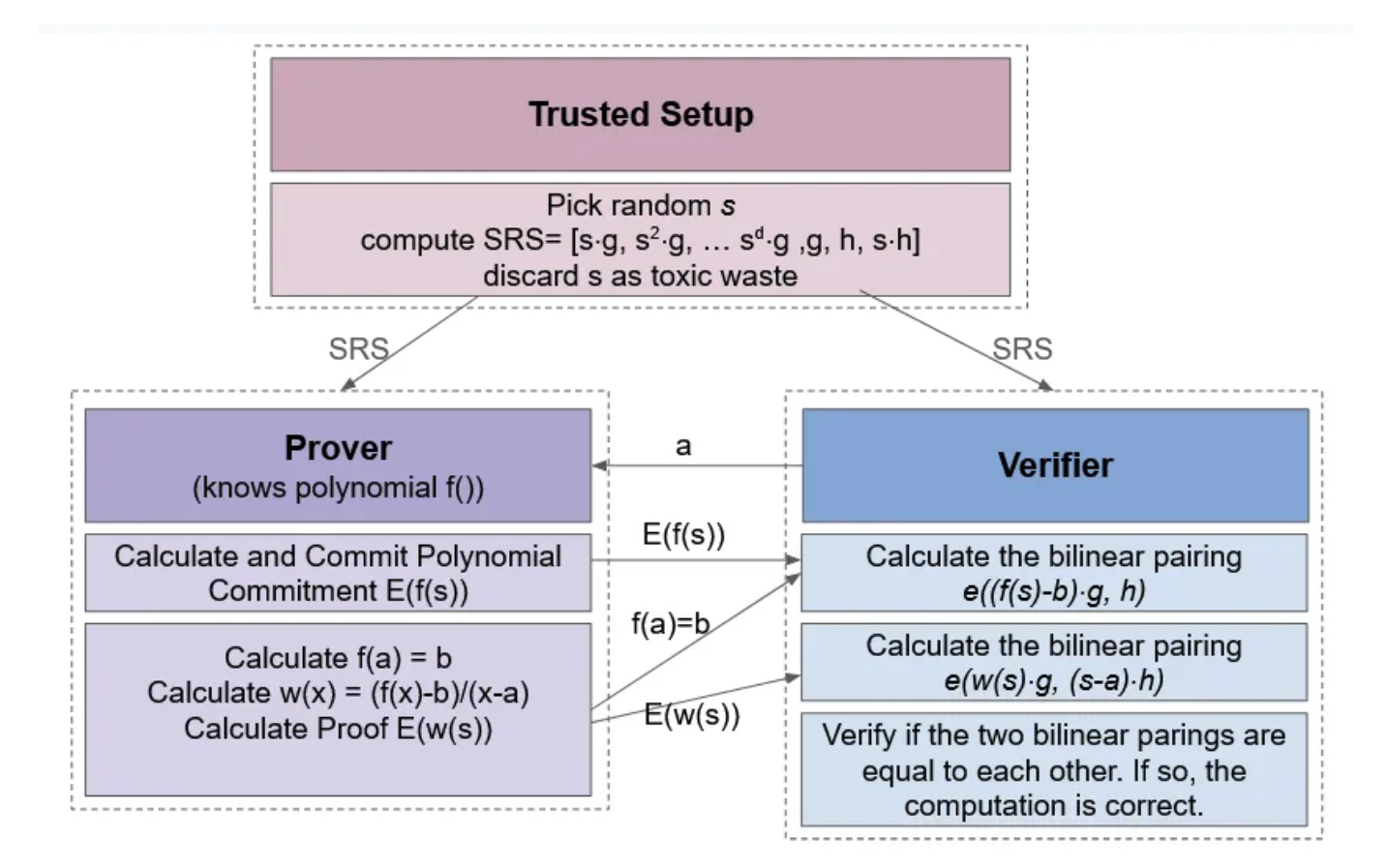
The ZKG Polynomial Commitment Scheme

可信设置：选择一个随机元素 s。考虑具有生成器 g 和 h 的椭圆曲线。计算并发布由 [g、s⋅g、s²⋅g、… s^d⋅g、h、s⋅h] 组成的标准参考字符串 (SRS)。然后将点 s 作为“有毒废物”丢弃（回想一下，不应允许证明者看到它）。

承诺：证明者必须承诺在点 s 处多项式 f(x) = sum_i (p_i * x^i) 的加密版本。这通过 E(f(s)) = sum_i (p_i ⋅(s^i⋅g)) 完成。请注意，证明者可以从 SRS 访问 s^i⋅g（对于所有 i），因此可以计算此多项式承诺。

函数评估和证明生成：当被要求为输入 a 生成输出时，首先计算输出 f(a) = b。然后，根据 f(x)、a、b 的知识，证明者能够计算商多项式函数 w(x) = (f(x)-b)/(x-a))。假设此函数的形式为 w(x) = sum_i (w_i * x^i)。证明者可以按如下方式计算此函数在点 s 处的加密求值：E(w(s)) = sum_i (w_i⋅(s^i⋅g))，我们将此数量视为证明。然后，证明者将求值 f(a) = b、多项式承诺 E(f(s)) 和证明 E(w(s)) 发送给验证者。

验证：验证者可以访问以下元素：f(a)=b、E(f(s)) 和 E(w(s)) 的求值。仅从这些元素来看，它旨在验证计算 w(s) = (f(s)-b)/(s-a)，或等效地，w(s)*(s-a) = f(s)-b。请注意，这个等式成立意味着证明者知道 f(x) 并已正确评估 f(a) = b。

困难在于验证者也不知道 s 或 f(s) 或 w(s)，只知道后两个多项式评估的加密版本。因此，此验证是通过使用合适的双线性配对来完成的。具体来说，它可以转换为检查以下两个双线性配对的相等性（回想一下第 3 部分，对于涉及具有生成器 P 和 Q 的群的双线性配对，我们得到 e(a⋅P,b⋅Q) = e(P,Q)^(ab) ):

e((f(s)-b)⋅g, h) = e(g,h)^(f(s)-b) ... (1)
e(w(s)⋅g, (s-a)⋅h) = e(g,h)^(w(s)(s-a)) … (2)

首先，请注意，验证者能够按如下方式计算 (1) 和 (2)。对于 (1)，第一项 (f(s)-b)⋅g 可以重写为 f(s)⋅g — b⋅g，并且验证者已经获得了 E(f(s)) = f(s)⋅g，这是加密的多项式承诺，以及来自证明者的值 b。并且它从 SRS 中知道 h。对于 (2)，它知道 E(w(s))=w(s)⋅g，因为这是证明者提供的证明，并且它可以计算 (s-a)⋅h = s⋅h -a⋅h，因为它有来自 SRS 的 s⋅h 和来自证明者的 a。

因此，如果两个计算相等，我们将得到 e(g,h)^(f(s)-b) = e(g,h)^(w(s)(s-a))，这意味着 f(s)-b = w(s)(s-a) 确实如此，这正是验证者需要检查的。如果它们不相等，那么证明者要么不知道多项式 f()，要么没有执行正确的计算 f(a)=b。如果它们相等，那么验证者可以放心，证明者确实用该函数进行了正确的计算。

KZG 的简洁性：请注意，多项式承诺 E(f(s)) 和证明 E(w(s)) 都只是具有生成器 g 的群 (椭圆曲线) 的一个元素。因此，无论多项式的次数如何，承诺和证明大小都保持不变。

KZG 在 zk-SNARK 中的应用：在本文中，我们重点讨论了证明者如何证明单个多项式函数的单次评估的正确执行的问题。证明通用程序的正确执行需要的远不止这些。我们应该提到，该方案可以轻松扩展以批量处理多个多项式。本文描述的 KZG 多项式承诺方案的变体构成了几种通用 zk-SNARK 方案的一部分，包括 Sonic、Marlin 和 PLONK。

下一篇文章：接下来，我们将看到如何将一般计算以算术电路的形式表示出来，然后转换为诸如秩一约束系统（R1CS）之类的表示，并进一步转换为二次算术程序（QAP），以便最终可以将它们表示为多项式，而多项式的评估需要在特定点进行验证。