【零知识证明】理解零知识证明：第二部分 - 密码学的数学基础

我们从上一篇文章开始本系列，该文章概述了零知识证明及其在实现可验证计算和保密性方面的作用。本系列的其余部分旨在阐明零知识证明的工作原理。对于刚接触密码学的人来说，要理解各种方案的工作原理，需要克服一些数学障碍。本文试图掌握一些基础知识，并提供更多学习指南。

域、群、椭圆曲线

域：域只是一组数字，配备了两个满足某些属性（即结合性、交换性、分配性、恒等式和逆元的存在性）的二进制运算（加法和乘法）。域的常见示例有理数集 (Q)、实数集 (R) 和具有 p 个元素的有限域 (Fp​)。

有限域：通常在密码学中使用有限域（也称为伽罗瓦域），元素的数量称为其顺序。域 Fp 由前 p 个整数组成：{0, 1, … (p-1)}。加法、减法和乘法等基本运算可以定义为整数，但使用模 p 运算，以便答案保持在集合内。除法的定义略有不同，以确保输出保持在域中，如下所示：x 除以 y 表示为 (x * y^(p-2) ) %p。

（一个有趣的题外话：为什么我们要用 x 乘以 y^(p-2) 来进行除法？首先请注意，直接用整数除法可能会得到非整数值：例如 1/2。费马小定理指出，对于 p 阶素域中的任何 y，y^p = y。由此我们可以看出 y^(p-1)*y= y，这意味着 y^(p-1)=1，这反过来又表明 y^(p-2)*y = 1，这表明 y^(p-2) 是 y 的逆。）

群：群是一个集合 G，它配备了满足闭包、结合律的二元运算（加法或乘法），具有单位元 e，并且每个元素都有一个逆元。如果存在一个元素 g∈G（称为生成元），使得 G 中的每个元素都可以写成 g^n（即，在乘法群的情况下，g 乘以 n 次）或 n⋅g（在加法群的情况下），其中 n 为整数，则群 G 称为循环群。所有循环群都是阿贝尔群（即运算是可交换的）。由任何有限域 Fp 形成的乘法群都是循环群。由任何具有素数阶的有限域形成的加法群也是循环群。拉格朗日定理指出，如果 G 是有限群，而 H 是 G 的子群，则 H 的阶（元素数）整除 G 的阶。该定理还表明，任何素数阶群都是循环群和简单群，因为由任何非恒等元素生成的子群必须是整个群本身。

椭圆曲线：椭圆曲线密码术 (ECC) 使用在有限域上定义的椭圆曲线的属性。有限域 Fp 上的椭圆曲线 E 由以下部分组成：
i) 所有满足方程 y² = x³+ax+b (mod p) 的点，其中 a 和 b 是满足条件 4a³ + 27b² (mod p) != 0 的常数，以及
ii) 称为 O 的“无穷远点”。

为了阐明它是什么样子，请考虑椭圆曲线 y² = x³+3 mod(11)。无穷远点以外的所有点都显示在下图中（来自此处）。

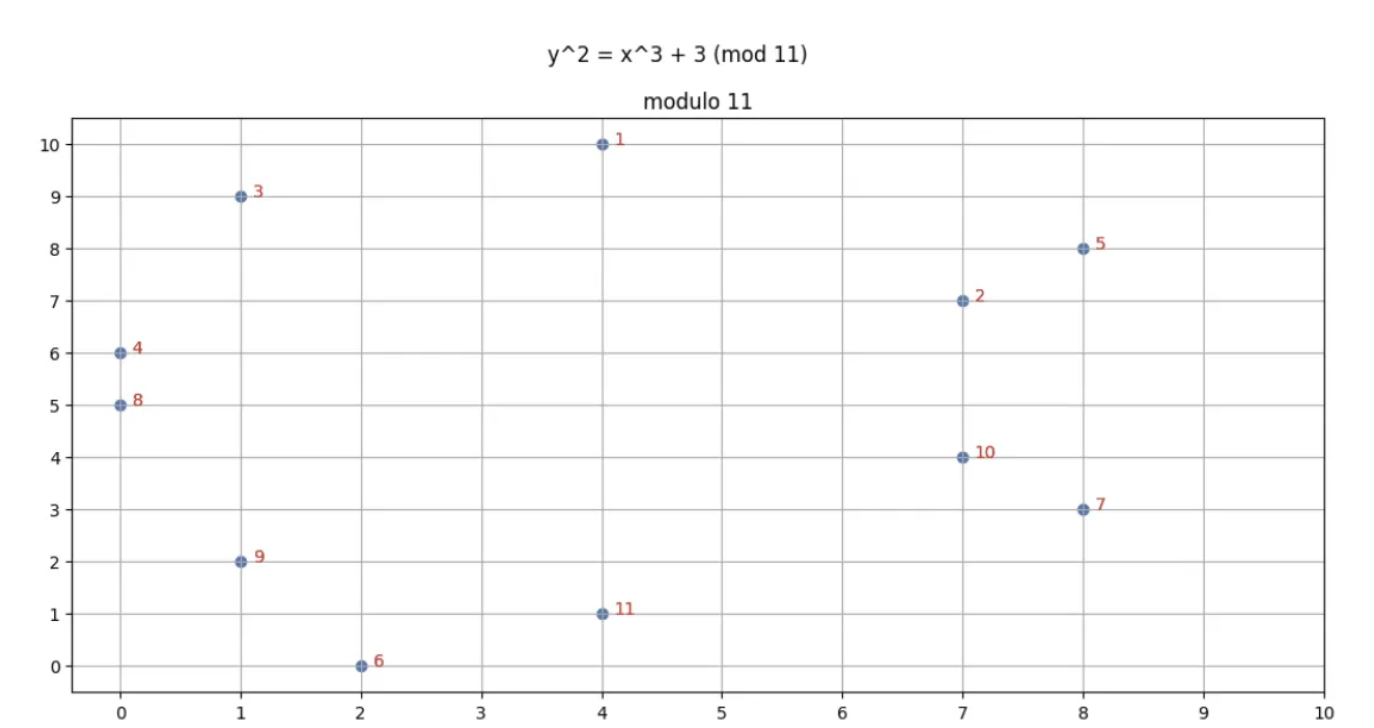
Illustration of an Elliptic Curve y² = x³ + 3, defined over F(11)

一种常用的椭圆曲线是 BN254，定义如下：

The elliptic curve BN254

椭圆曲线和群：椭圆曲线有一个特殊的几何定义加法算子。下图展示了实数上的椭圆曲线。

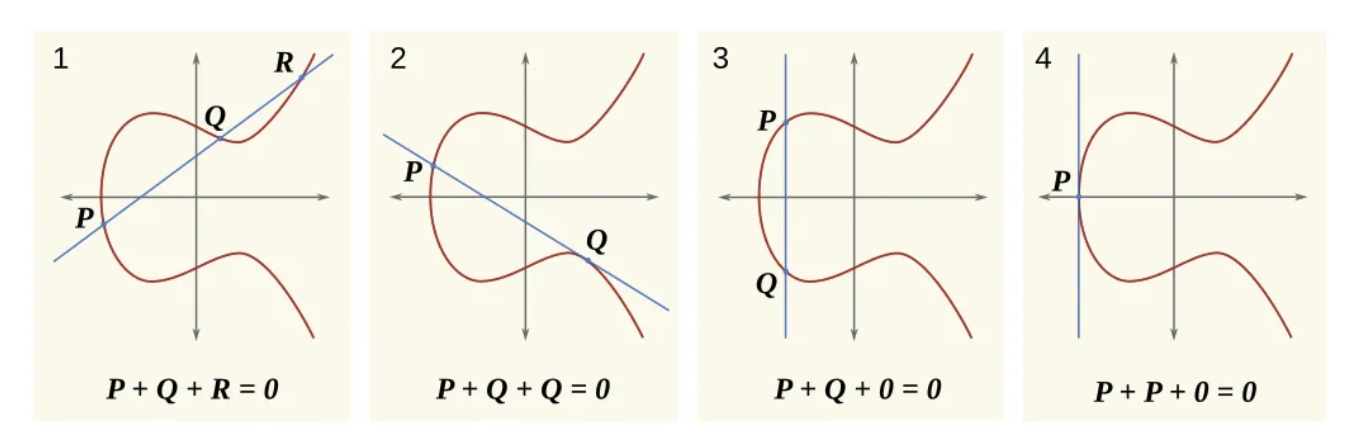
Illustrating the addition operation on an Elliptic Curve over Reals (from Wikipedia)

也可以为有限域上的椭圆曲线定义类似的操作，如下所示。

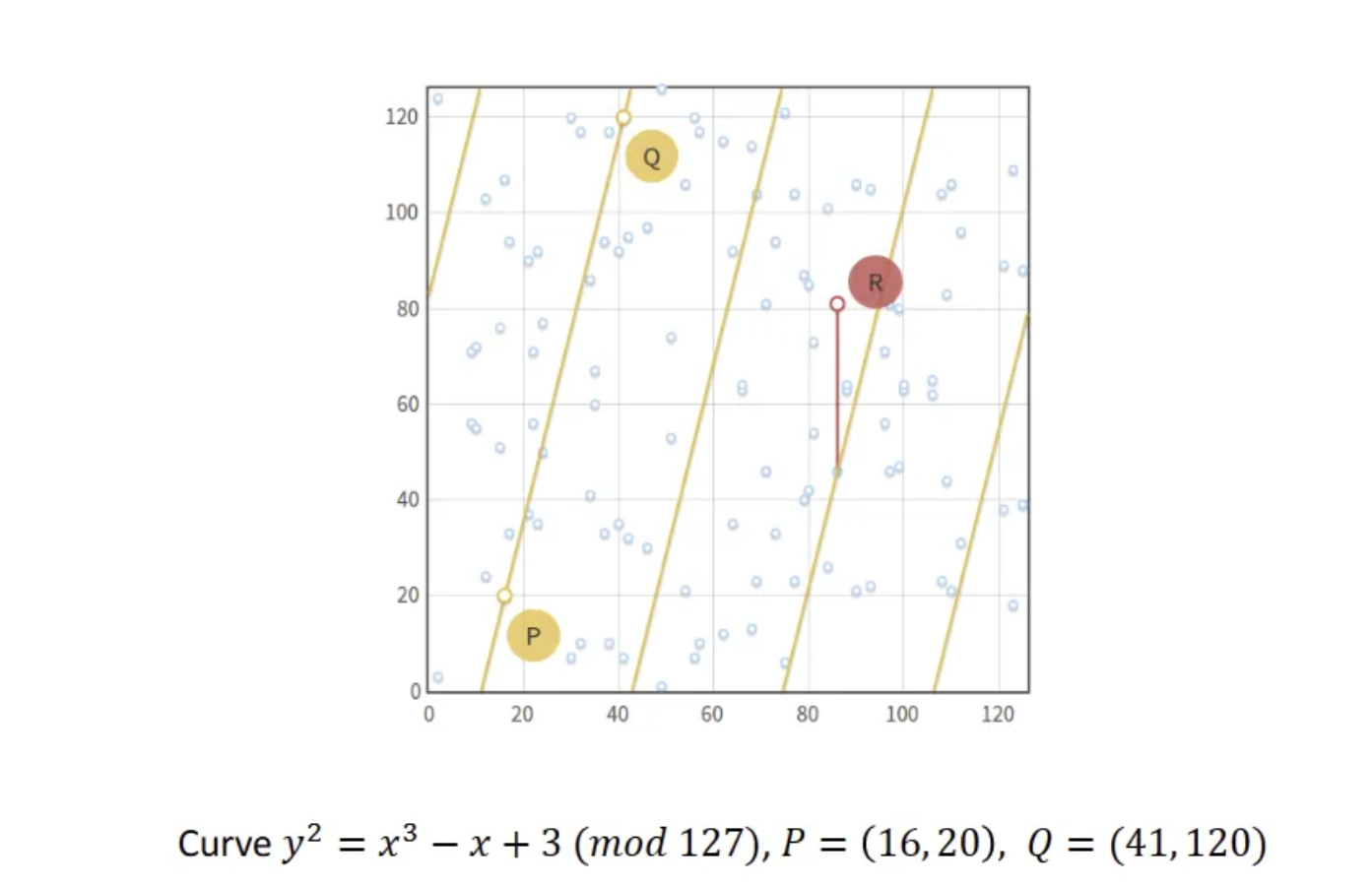
Illustrating P+Q+R=0 for a particular Elliptic Curve over the finite field F(127). Source lecture notes on Elliptic Curve Cryptography by Anupam Datta.

有限域上的椭圆曲线上的所有点的集合，我们称之为 E{Fp}，加上上述加法运算符，形成一个加法群。将曲线 P 上的任何基点视为生成器，我们得到一个循环加法群，其特性是该群中的所有其他元素都可以生成为生成器的整数倍，即 n⋅P 形式。

给定一个在有限域 Fq​ 上定义的椭圆曲线，可以找到一个基点，该基点生成一个具有最大素数阶 r 的循环子群，其中 r 是 E{Fq} 阶的最大素因子。此循环加法子群通常用于椭圆曲线密码学。

使用椭圆曲线的一个好处是可以非常快速地完成各种运算，例如加法、加倍、取反以及将点乘以标量。