【强化学习】强化学习，第6部分：TD（λ）和Q-学习 |

语言 Chinese, Simplified

SEO Title

Reinforcement Learning, Part 6: TD(λ) & Q-learning

时间差异学习：TD（λ）

在我上一篇文章中，我们提到，如果我们用估计的返回值Rt+1+V（St+1）替换MC更新公式中的Gt，我们可以得到TD（0）：

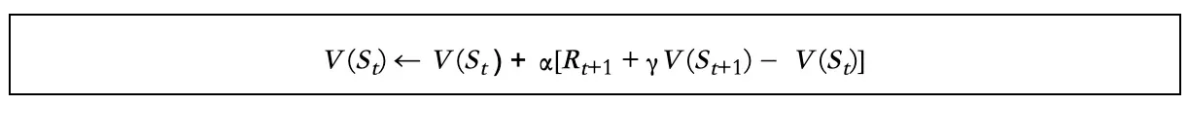
哪里：

Rt+1+V（St+1）称为TD目标值
Rt+1+V（St+1）-V（St）称为TD误差

现在，我们用Gt（）替换TD目标值，我们可以得到TD（λ）。Gt（）的生成过程如下：

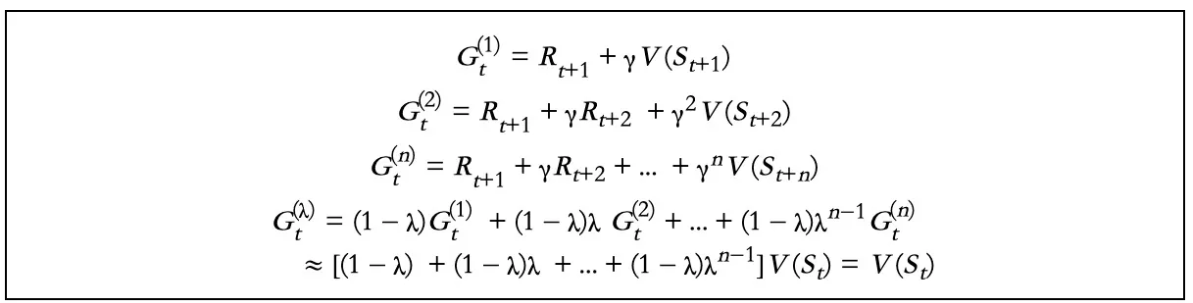
因此，TD（λ）公式为：

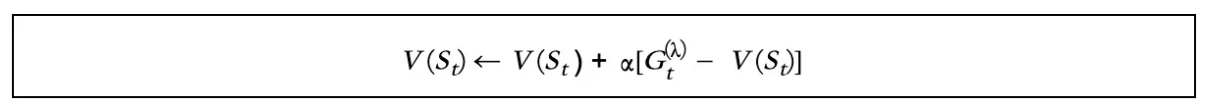
在哪儿：

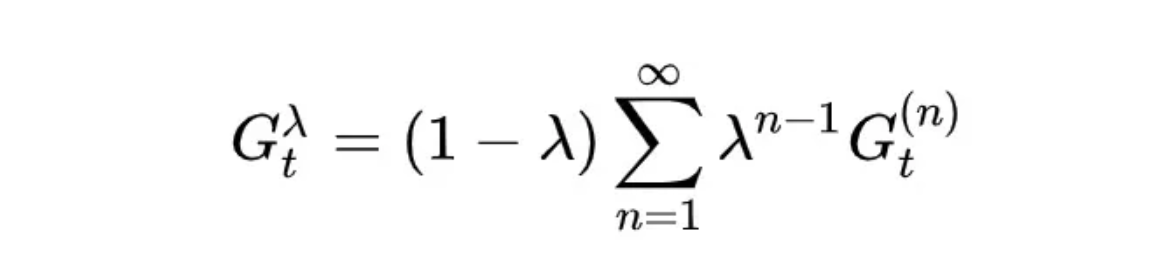
如前所述，Q学习是蒙特卡洛（MC）和时间差分（TD）学习的结合。随着MC和TD（0）在第5部分中的介绍以及TD（λ）的介绍，我们终于准备好拿出大炮了！

Q学习

Q值公式：

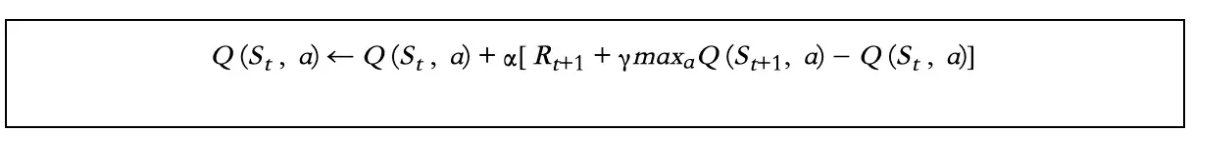
从上面可以看出，Q学习是直接从TD（0）导出的。对于每一个更新的步骤，Q-learning都采用贪婪的方法：maxaQ（St+1，a）。

这是Q-learning和另一种基于TD的方法Sarsa之间的主要区别，我在本系列中不会解释。但作为强化学习者，你应该知道Q-learning并不是基于TD的唯一方法。

Q-Learning的工作原理示例

让我们通过一个例子来更好地理解这一点：

你和朋友在一家意大利餐厅吃饭，因为你以前来过一两次，他们想让你点餐。根据经验，你知道玛格丽塔披萨和博洛尼亚意大利面很美味。所以，如果你必须点十道菜，经验可能会告诉你每道菜点五道。但是菜单上的其他东西呢？

在这种情况下，你就像我们的“代理人”，负责找到十道菜的最佳组合。想象一下，这变成了每周的晚餐；你可能会开始带一个笔记本来记录每道菜的信息。在Q学习中，代理在Q表中收集Q值。对于餐厅菜单，你可以把这些值看作是每道菜的分数。

现在，假设你的聚会第三次回到餐厅。你的笔记本上现在有一些信息，但你肯定还没有浏览过整个菜单。你如何决定从你的笔记中点多少道菜——你知道哪些菜很好，又点多少道新菜？

这就是ε-贪婪发挥作用的地方。

ε-贪婪的勘探政策

在上面的例子中，餐厅发生的事情就像我们的MDP（马尔可夫决策过程），而你作为我们的“代理人”，只有充分探索，才能为你的聚会找到最佳的菜肴组合。

Q-Learning也是如此：只有当代理足够彻底地探索MDP时，它才能工作。当然，这将需要非常长的时间。你能想象有多少次你必须回到餐厅尝试菜单上每一道菜的每一种组合吗？

这就是为什么Q-learning使用ε-贪婪策略，即ε度“贪婪”用于最高Q值，1--ε度“贪吃”用于随机探索。

在训练代理的初始阶段，随机探索环境（即尝试菜单上的新事物）通常比固定行为模式（即订购你已经知道的好东西）更好，因为这是代理积累经验并填满Q表的时候。

因此，ε通常以高值开始，例如1.0。这意味着代理将花费100%的时间进行探索（例如使用随机策略），而不是参考Q表。

从那里，ε的值可以逐渐减小，使代理对Q值更加贪婪。例如，如果我们将ε降至0.9，这意味着代理将花费90%的时间根据Q表选择最佳策略，10%的时间探索未知。

与完全贪婪策略相比，ε-贪婪策略的优点是它总是不断测试MDP的未知区域。即使目标策略看起来是最优的，算法也从未停止探索：它只是越来越好。

勘探有各种功能，可以在网上找到许多已定义的勘探策略。请注意，并非所有的探索策略都适用于离散和连续的行动空间。

Q-Learning的Python实现

以下是Q-learning的实现方式：

import numpy as np
# Q
q = np.matrix(np.zeros([6, 6]))
# Reward
r = np.matrix([[-1, -1, -1, -1,  0,  -1],
[-1, -1, -1,  0, -1, 100],
[-1, -1, -1,  0, -1,  -1],
[-1,  0,  0, -1,  0,  -1],
[ 0, -1, -1,  0, -1, 100],
[-1,  0, -1, -1,  0, 100]])
gamma = 0.8
epsilon = 0.4
# the main training loop
for episode in range(101):
# random initial state
state = np.random.randint(0, 6)
# if not final state
while (state != 5):
# choose a possible action
# Even in random case, we cannot choose actions whose r[state, action] = -1.
possible_actions = []
possible_q = []
for action in range(6):
if r[state, action] >= 0:
possible_actions.append(action)
possible_q.append(q[state, action])
# Step next state, here we use epsilon-greedy algorithm.
action = -1
if np.random.random() < epsilon:
# choose random action
action = possible_actions[np.random.randint(0, len(possible_actions))]
else:
# greedy
action = possible_actions[np.argmax(possible_q)]
# Update Q value
q[state, action] = r[state, action] + gamma * q[action].max()
# Go to the next state
state = action
# Display training progress
if episode % 10 == 0:
print("------------------------------------------------")
print("Training episode: %d" % episode)
print(q)

给定足够的迭代次数，该算法将收敛到最优Q值。这被称为非策略算法，因为正在训练的策略不是正在执行的策略。

注：以上代码来自https://blog.csdn.net/zjm750617105/article/details/80295267